2-2. 電化學交流阻抗全解析
交流阻抗(AC Impedance)也稱做電化學阻抗圖譜(Electrochemical Impedance Spectroscopy, EIS),其方法為在一個電化學系統中施予一個改變頻率的交流電位,並量測其交流電流訊號,而得以計算此電化學系統之阻抗值,並透過以電路元件所組成的等效電路,得以表達此電化學系統於電極介面所發生的電化學反應。
2-2-1. 直流電位 (固定電壓) vs 交流電位 (正弦訊號)
當對一個電化學系統施加固定電壓的直流電位時,如在章節1-2-2-4所介紹的安培法(Amperometry, IT),可以觀察到電流值經過一小段不穩定態的變化時間,隨後會進入穩定態,成為固定值的水平線。
.webp) 圖 2-2-1 (a). 固定電壓直流電位與直流電流訊號
圖 2-2-1 (a). 固定電壓直流電位與直流電流訊號透過適當調整施加的電壓,可以由量測所得電流值,對系統中特定的物質反應進行定性與定量分析。然而直流電位的分析方式一般只能提供特定化學反應的相關資訊,而無法更詳細描述在整個電化學系統中所發生的行為。 而在施加交流電位的情況下,就如同將系統維持在前述的變化時間,可以更動態地偵測系統中發生的現象,如蓄電結構的充放電、離子的擴散運動等。
交流阻抗量測中所施加的交流電位,一般以單一正弦波為例,可以表達為:
e(t) = E sin (ωt) .webp) 圖 2-2-1 (b). 單一正弦波交流電位
圖 2-2-1 (b). 單一正弦波交流電位 其中E為振幅、ω為角頻率(頻率f的2π倍,單位為弧度每秒)、t為時間。
而量測到的交流電流同樣可以表達為:
i(t) = I sin (ωt + Ψ).webp) 圖 2-2-1 (c). 交流電位與交流電流訊號
圖 2-2-1 (c). 交流電位與交流電流訊號.webp)
圖 2-2-1 (d). 相位角示意圖
其中I為振幅、Ψ為電流與電位的相位差對應的相位角(phase angle, φ)。 相位差的概念,是系統的交流電流並不一定與施加的交流電位同步達到峰值,由於系統中可能會有類似電容的充放電結構,或者有類似電感對電流形成抵抗的效應,便會導致電流訊號先於電壓出現或晚於電壓出現,稱之為電流領先或是落後電壓。如上圖2-2-1 (c)即為電流領先電壓的示意圖。
2-2-2. 阻抗 (Impedance)
已知施加的交流電位,並且測得交流電流訊號,透過歐姆定律(Ohm’s Law):
E = I R
Z = e(t) / i(t)
即可求得此電化學系統之交流阻抗(Z, Impedance),此阻抗包含其阻抗大小以及造成的相位差,即|Z|和∠Ψ,常會使用複數平面,透過向量的方式更清楚表達,即由實部(real parts, Zre)和虛部(imaginary parts, Zim)所組成。由於將使用複數平面,以下對此部分使用尤拉公式(Euler's formula)進行轉換與推導:
Euler’s formula: ejωt = cos(ωt) + j sin(ωt) (e為自然底數)
將e(t) = E sin(ωt) 轉換為e(t) = E cos(ωt-π/2) + j E sin(ωt-π/2) = E ej(ωt-π/2)
同樣將i(t) = I sin (ωt + Ψ) 轉換為 i(t) = I ej(ωt-π/2+Ψ)
Z = e(t) / i(t) = (E ej(ωt-π/2)) / (I ej(ωt-π/2+Ψ)) = E/I ej(-Ψ) = |Z| ej(-Ψ)
Z = |Z| cos(-Ψ) + j |Z| sin(-Ψ) = |Z| cos(Ψ) – j |Z| sin(Ψ)
Z = Zre – j Zim
.webp) 圖 2-2-2 (a). 複數平面上的交流阻抗
圖 2-2-2 (a). 複數平面上的交流阻抗由於系統的交流阻抗會對應不同頻率而有變化,因此電化學阻抗圖譜方法就是對系統施加不同頻率的交流電位,量測其電流變化,並透過以上計算得到在不同頻率下的交流阻抗,如下圖2-2-2 (b)所示:
.webp) 圖 2-2-2 (b). 交流阻抗之實部與虛部,與頻率以三維方式作圖
圖 2-2-2 (b). 交流阻抗之實部與虛部,與頻率以三維方式作圖建立此交流阻抗與頻率的關係後,即可透過以下章節將介紹的分析方式,進一步了解該電化學系統。
2-2-3. 等效電路與電路元件
由於電化學系統中,電極表面的物理性質與化學反應多樣而複雜,因此常會使用等效電路的方式,以不同特性的簡單電路元件表達具有相似特性的物理化學現象,藉此以理解整個系統。
一般於等效電路中所使用的電路元件有三種,包含電阻、電容與電感。
2-2-3-1. 電阻 (Resistance)
電阻為電路中對電流/電子流的阻礙能力,電阻值表達為R,單位為歐姆(Ω)。在等效電路中使用符合歐姆定律之E = I R,即電阻的阻抗ZR = R。此阻抗與頻率無關,並不造成電位與電流的相位差,即相位差為0°,為純實部阻抗。
在電化學系統中,當電流通過不同的物質或是介面,而受到不同的阻礙能力,便可以電阻形式在等效電路中表達。
.webp) 圖 2-2-3-1 (a). 電阻的交流電位與交流電流示意圖
圖 2-2-3-1 (a). 電阻的交流電位與交流電流示意圖.webp)
圖 2-2-3-1 (b). 不造成相位差
2-2-3-2. 電容 (Capacitance)
電容為電路中給定電位時儲存電荷(q)的能力,電容值表達為C,單位為法拉(F)。電容在一般電路中以兩塊平行電極板理解,電容、電荷與電位的關係可以表達為:
q = C v
透過電流與電荷的關係可得:
i = dq/dt
i = C dv/dt
當電位為單一正弦波時,可得電容的阻抗ZC = 1 / jωC。此阻抗隨頻率越高則則阻抗越低,並造成電流領先電壓90°的相位差,為純虛部阻抗。 在簡易的電路分析中,可以視電容為高頻時短路、低頻時斷路之元件。 在電化學系統中,當介面之間具有分層的現象,且進而產生蓄積電荷的情形,便可以電容形式在等效電路中表達。
.webp) 圖 2-2-3-2 (a). 電容的交流電位與交流電流示意圖
圖 2-2-3-2 (a). 電容的交流電位與交流電流示意圖.webp)
圖 2-2-3-2 (b). 電流領先 90°
2-2-3-3. 電感 (Inductance)
電感為電路中因通過電流時產生的磁通量(φ)與感應電動勢,而抵抗電流變化的能力,電感值表達為L,單位為亨利(H)。電感在一般電路中以數匝線圈理解,電感、電流、磁通量與線圈匝數(N)的關係可以表達為:
N φ = L i
透過感應電動勢與磁通量的關係可得:
v = N dφ/dt
v = L di/dt
當電位為單一正弦波時,可得電感的阻抗ZL = jωL。此阻抗隨頻率越高則阻抗越高,並會造成電流落後電壓90°的相位差,為純虛部阻抗。 在簡易的電路分析中,可以視電感為高頻時斷路、低頻時短路之元件。 在電化學系統中,若有因通過電流產生磁通量與感應電動勢,進而產生抵抗電流變化的情形,便可以電感形式在等效電路中表達。
.webp) 圖 2-2-3-3 (a). 電感的交流電位與交流電流示意圖
圖 2-2-3-3 (a). 電感的交流電位與交流電流示意圖.jpg)
圖 2-2-3-3 (b). 電流落後90°
電阻、電容以及電感的比較如下表:
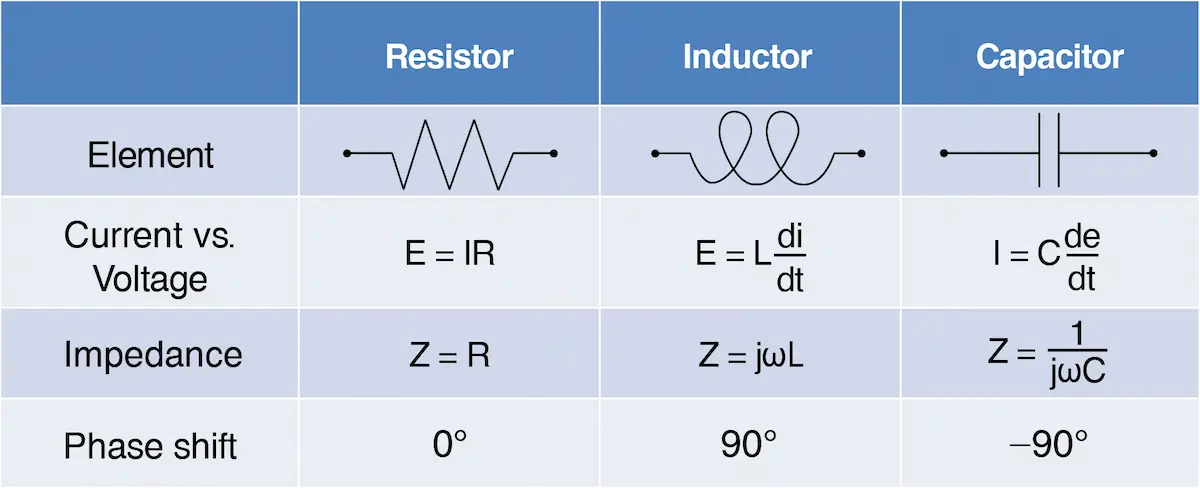 表 2-2-3. 電阻、電容以及電感比較
表 2-2-3. 電阻、電容以及電感比較2-2-4. 奈奎斯特圖(Nyquist plot)與波德圖(Bode plot)
在章節2-2-2中介紹過,交流阻抗方法所得的結果可以三維方式作圖表達,其三軸分別為頻率frequency(或角頻率ω,此軸通常以對數座標呈現)、實部阻抗Z’以及虛部阻抗Z’’,如圖2-2-4所示:
.webp) 圖 2-2-4(a). 交流阻抗之實部與虛部,與頻率以三維方式作圖,其中A面即為奈奎斯特圖,B面及C面雖非波德圖,但為相似的表達方式,可以應分析需求使用;而|Z|和Ψ對頻率作圖則為波德圖(D與E)
圖 2-2-4(a). 交流阻抗之實部與虛部,與頻率以三維方式作圖,其中A面即為奈奎斯特圖,B面及C面雖非波德圖,但為相似的表達方式,可以應分析需求使用;而|Z|和Ψ對頻率作圖則為波德圖(D與E).webp) 圖 2-2-4(b). 以電阻電容並聯電路之實際量測,示範在圖2-2-4(a)中,A~E各圖形
圖 2-2-4(b). 以電阻電容並聯電路之實際量測,示範在圖2-2-4(a)中,A~E各圖形而二維方式作圖則常見以奈奎斯特圖與波德圖表達。奈奎斯特圖是以實部阻抗為x軸、虛部阻抗為y軸而隱含其頻率訊息的作圖方式,如圖2-2-4中的A面。而波德圖是以頻率或角頻率為x軸、總阻抗大小(|Z|, 有時會以對數座標軸或Log|Z|方式呈現)及相位角(φ)為y軸作圖。
以下將以電阻及電容所組成簡單電路為例,繪製其奈奎斯特圖與波德圖。
2-2-4-1. 純電阻
純電阻電路只有實部阻抗而沒有虛部阻抗,且其值不隨角頻率變化,亦不造成相位差。故其於奈奎斯特圖上僅有實部x軸上一點,其值為電阻值R。而在波德圖上則為一y值阻抗為R的水平線,以及一y值相位差為0°的水平線。
.webp)
圖 2-2-4-1 (a). 純電阻電路之理論奈奎斯特圖與波德圖
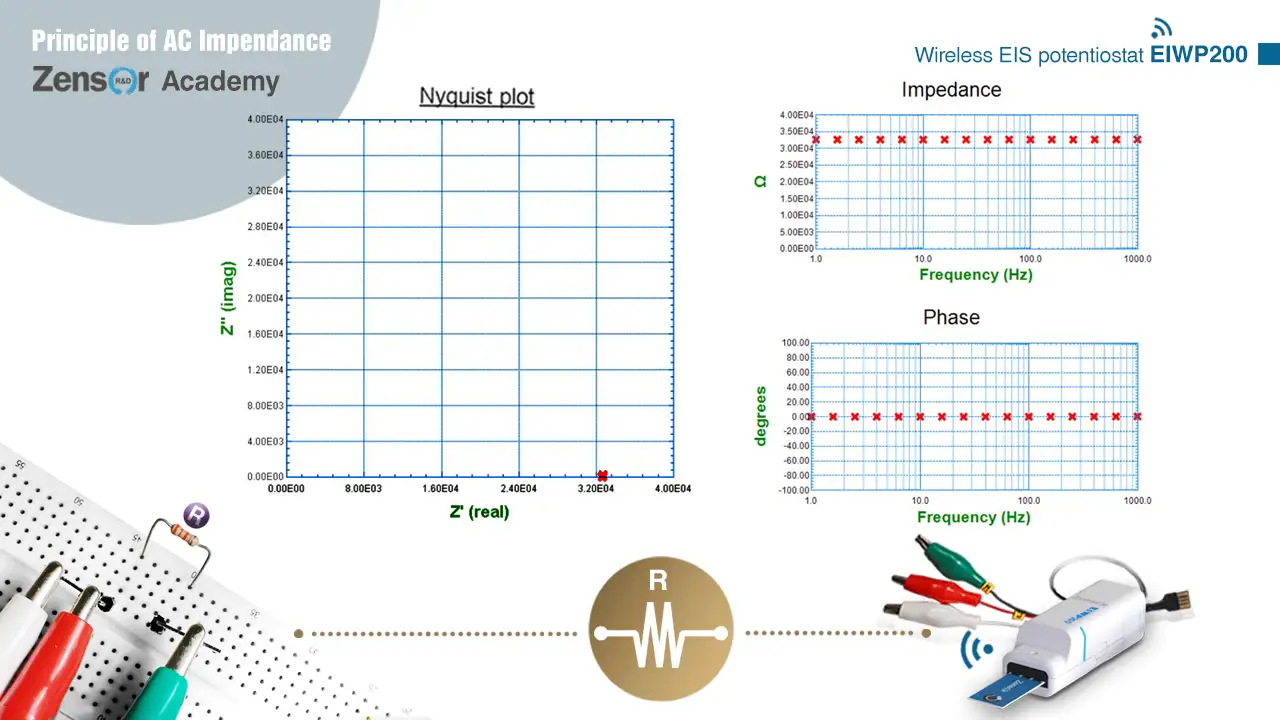
圖2-2-4-1 (b) 純電阻電路之實際量測奈奎斯特圖與波德圖
2-2-4-2. 純電容
純電容電路只有虛部阻抗而沒有實部阻抗,其值隨角頻率越高則越趨近於0,並造成-90°的相位差。故其於奈奎斯特圖上為與y軸重疊之直線。而在波德圖上則為一y值阻抗為低頻較高、高頻為0之斜線,以及一y值相位差為90°的水平線。
圖 2-2-4-2 (a). 純電容電路之理論奈奎斯特圖與波德圖
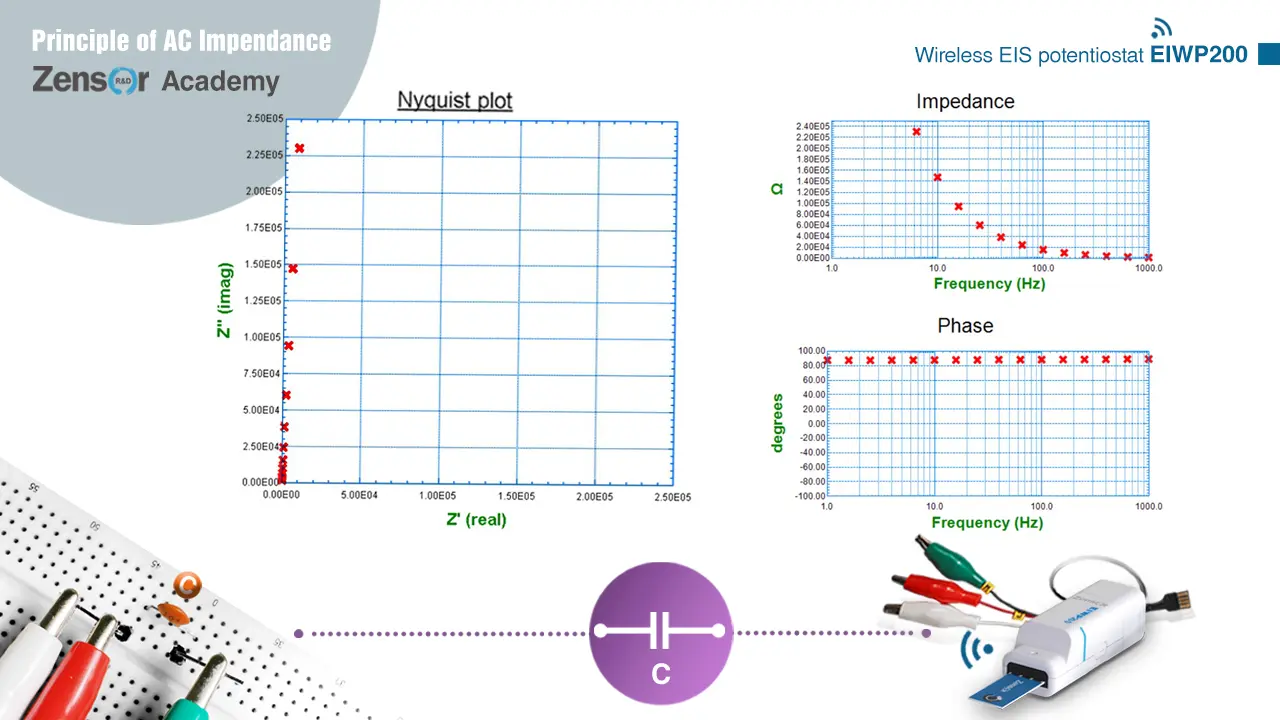
圖 2-2-4-2 (b). 純電容電路之實際量測奈奎斯特圖與波德圖
2-2-4-3. 串聯
電阻與電容串聯時,阻抗為兩者相加,故其阻抗值為R + 1 / jωC。在奈 奎斯特圖上即為x = R 之直線。而在波德圖上則為一y 值阻抗為低頻較 高、高頻為R 之曲線,以及一y 值相位差為低頻為90°、高頻為0°之 曲線。
圖 2-2-4-3 (a). 電阻與電容串聯電路之理論奈奎斯特圖與波德圖 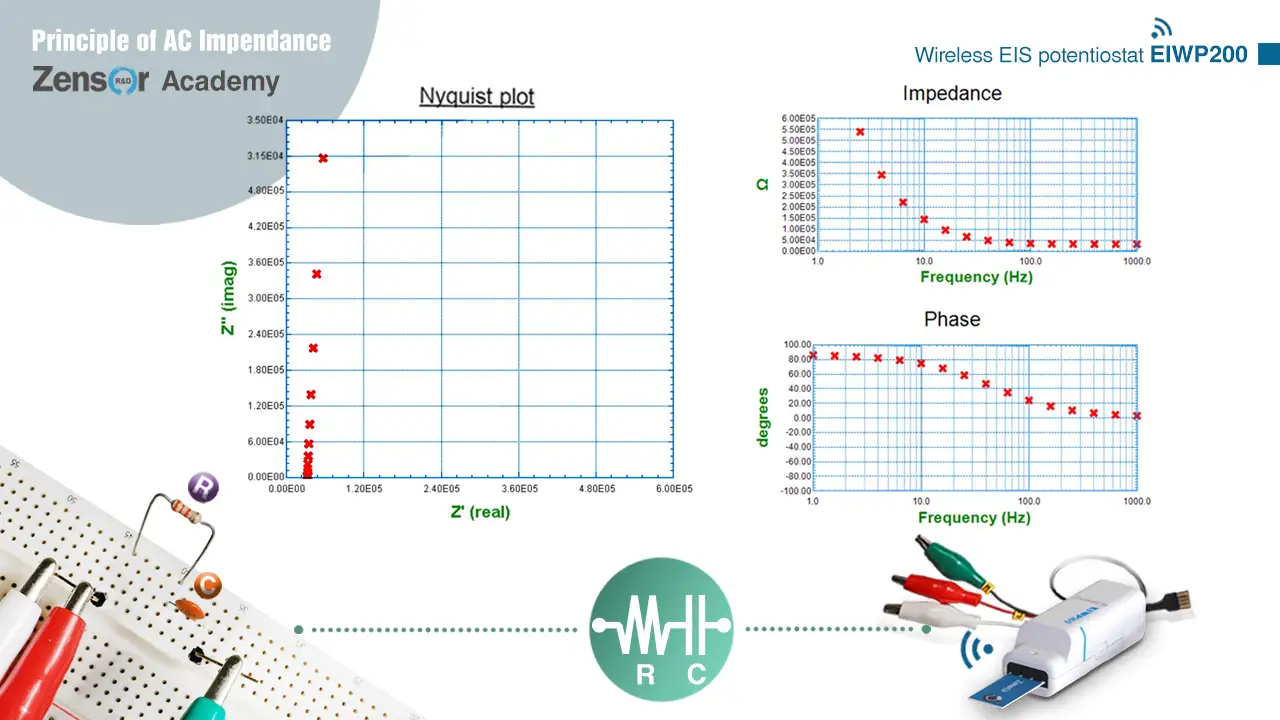 圖 2-2-4-3 (b). 電阻與電容串聯電路之實際量測奈奎斯特圖與波德圖
圖 2-2-4-3 (b). 電阻與電容串聯電路之實際量測奈奎斯特圖與波德圖2-2-4-4. 並聯
電阻與電容並聯時,阻抗倒數為兩者倒數相加,其阻抗值推導如下:
1/Z = 1/R + 1/(1/jωC) = (jωRC + 1) / R
Z = R / (jωRC + 1) = (R – jωR2C) / (ω2R2C2 + 1)
在奈奎斯特圖上其為一個高頻端接近(0, 0)、低頻端為(R, 0)之半圓形。而在波德圖上則為一y值阻抗為低頻為R、高頻為0之曲線,以及一y值相位差為低頻為0、高頻為90°之曲線。
圖 2-2-4-4 (a). 電阻與電容並聯電路之理論奈奎斯特圖與波德圖 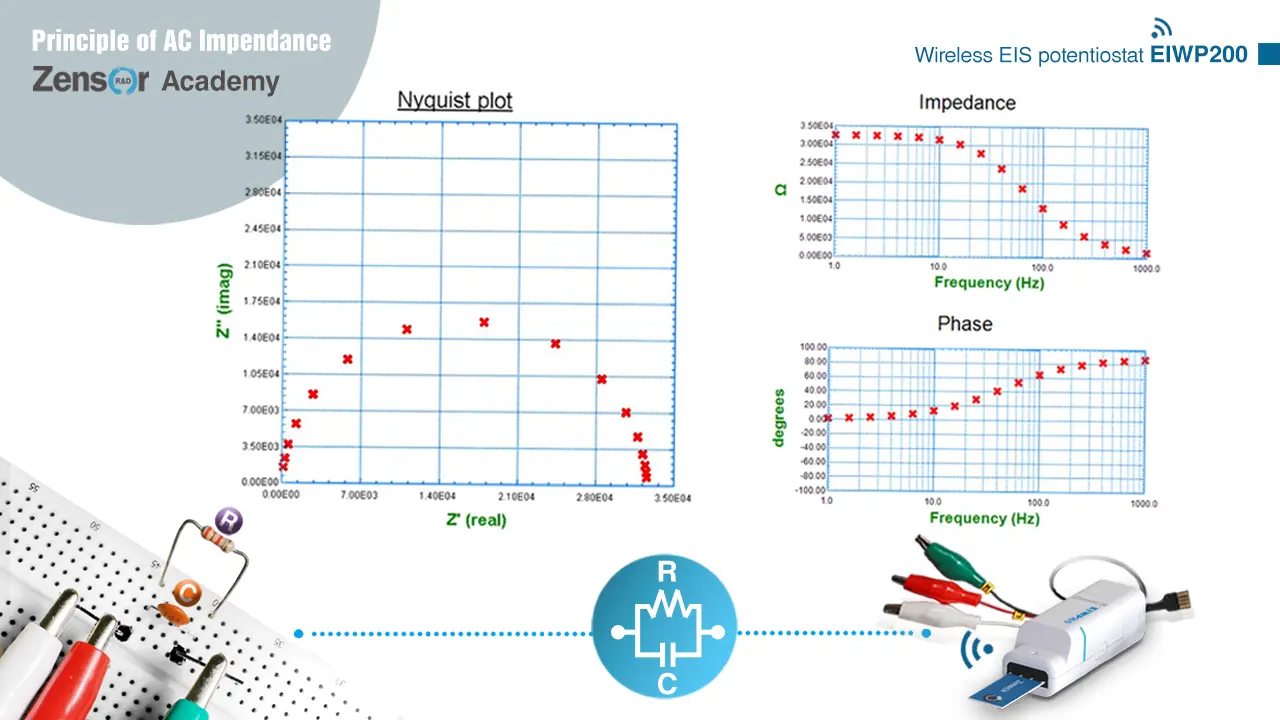 圖 2-2-4-4 (b). 電阻與電容並聯電路之實際量測奈奎斯特圖與波德圖
圖 2-2-4-4 (b). 電阻與電容並聯電路之實際量測奈奎斯特圖與波德圖2-2-5. 電化學系統與等效電路之對應 (以Randles equivalent circuit為例)
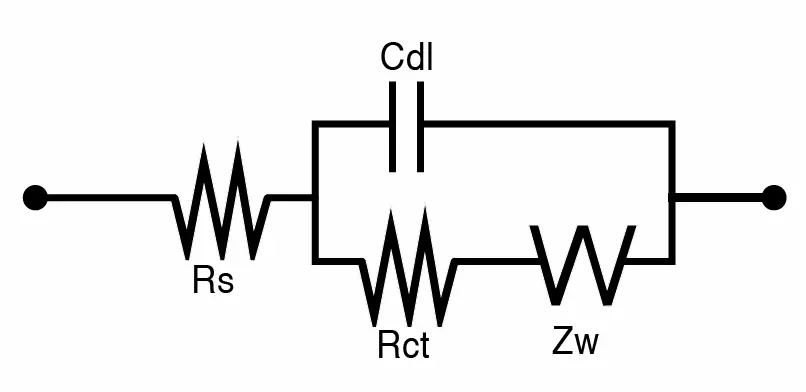
電化學系統所使用的等效電路中,常見Randles equivalent circuit,其等效電路組成如下圖:
.webp) 圖 2-2-5 (c). Randles equivalent circuit高頻簡化之等效電路與奈奎斯特圖
圖 2-2-5 (c). Randles equivalent circuit高頻簡化之等效電路與奈奎斯特圖圖 2-2-5 (a).Randles equivalent circuit對應電化學系統
其中Rs表示電解液之電阻值、Cdl表示電雙層(double layer)的電容特性、Rct表示在電極表面上的電化學活性物質(O or R) ,因為電化學反應而產生的電荷轉移(charge transfer)之電阻值,Cdl與Rct是與電極表面所發生之電化學反應最主要相關的項目。
Zw (Warburg impedance) 則是隨頻率變動之離子擴散(ion diffusion)阻抗,當頻率較高時,系統中的離子無法及時隨電極電位改變方向而移動,故此阻抗不顯著;而當頻率較低時,離子便有足夠時間可以隨電極電位而被吸引或排斥,因此產生具有電荷移動以及充放電的現象。Zw在等效電路上亦可視為無數個電阻電容並聯的串聯,如下圖所示:
.webp) 圖 2-2-5 (b). Warburg impedance的等效電路
圖 2-2-5 (b). Warburg impedance的等效電路一般在等效電路中僅以Zw表示,因其具有電阻和電容的特性,故由實部阻抗與虛部阻抗共同組成,其公式表達為:
Zw = Aw/√ω + Aw/j√ω
其中Aw是Warburg係數(Warburg coefficient),此係數與系統中的離子濃度、擴散係數以及溫度等離子擴散的條件相關。由Zw的公式可見其為一個固定相位為-45°的原件,因此在奈奎斯特圖上可以看見一條45°的斜直線,即是受到Zw的影響。
當頻率較高時,Zw不顯著,等效電路由Cdl並聯Rct再串聯Rs所主導,而當頻率極高時更可以視為只有Rs,故可知在奈奎斯特圖上,其高頻區段為一半圓,高頻端為Rs而低頻端為Rs + Rct,如下圖所示:
左圖.webp) 圖 2-2-5 (c). Randles equivalent circuit高頻簡化之等效電路與奈奎斯特圖
圖 2-2-5 (c). Randles equivalent circuit高頻簡化之等效電路與奈奎斯特圖當頻率較低時,Cdl視為斷路,等效電路由Rs、Rct與Zw串連所主導,由於Zw固定相位的特性,在奈奎斯特圖上會呈現一條與x軸夾角為45°的斜直線,如下圖所示:
圖 2-2-5 (d). Randles equivalent circuit低頻簡化之等效電路與奈奎斯特圖綜合以上,可得Randles equivalent circuit的總體奈奎斯特圖如下:
圖 2-2-5 (e). Randles equivalent circuit與綜合高頻與低頻所得之理論等效電路與奈奎斯特圖2-2-6. 電化學系統與等效電路之對應實例
Randles equivalent circuit 雖然常見於電化學系統所對應的等效電路,但系統 往往更為複雜,因此實驗者需要對其操做的系統反應有一定程度的了解,方能建 立有效的電路模型以與實驗量測的成果相對應。此章節以薄膜修飾電極之文獻舉 例如下圖: 圖
右圖-11.webp)
圖 2-2-6 (a). 薄膜修飾電極之等效電路對應電化學系統 [1]
其中Rs 為溶液電阻,Rct 與CPE (理想狀態為Cdl,與電極表面粗糙度相關)為 薄膜與電極介面阻抗,ZD 相當於Warburg 元件代表薄膜內的擴散行為,此四項可 以由章節2-2-5 的Randles equivalent circuit 模型理解。
而Cb (bulk capacitance)與Rb (bulk resistance)為薄膜介電質特性,Cfs 與Rfs 則 為系統中離子為了維持電中性而進出薄膜造成的阻抗。 此等效電路所得之奈奎斯特圖如下: 圖
右圖-11.webp) 圖 2-2-6 (b). 薄膜修飾電極之奈奎斯特圖 [1]
圖 2-2-6 (b). 薄膜修飾電極之奈奎斯特圖 [1]圖中可以觀察到第一個半圓由薄膜介電質特性(Cb 與Rb)所主導,第二個半圓 由薄膜與電極介面(CPE 與Rct)所主導,接著ZD 呈現具有Warburg 特徵的45∘斜 直線,最後在低頻端受到薄膜電容特性影響而呈現垂直線。 參
參考文獻[1] Jyh-Myng Zen,* Govindasamy Ilangovan, and Jia-Jen Jou, Anal. Chem. 1999, 71, 2797-2805
Next Article →














.webp) 圖 2-2-1 (a). 固定電壓直流電位與直流電流訊號
圖 2-2-1 (a). 固定電壓直流電位與直流電流訊號.webp) 圖 2-2-1 (b). 單一正弦波交流電位
圖 2-2-1 (b). 單一正弦波交流電位.webp)
.webp)
.webp)
.webp) 圖 2-2-2 (b). 交流阻抗之實部與虛部,與頻率以三維方式作圖
圖 2-2-2 (b). 交流阻抗之實部與虛部,與頻率以三維方式作圖.webp)
.webp)
.webp) 圖 2-2-3-2 (a). 電容的交流電位與交流電流示意圖
圖 2-2-3-2 (a). 電容的交流電位與交流電流示意圖.webp)
.webp)
.jpg)
 表 2-2-3. 電阻、電容以及電感比較
表 2-2-3. 電阻、電容以及電感比較.webp) 圖 2-2-4(a). 交流阻抗之實部與虛部,與頻率以三維方式作圖,其中A面即為奈奎斯特圖,B面及C面雖非波德圖,但為相似的表達方式,可以應分析需求使用;而|Z|和Ψ對頻率作圖則為波德圖(D與E)
圖 2-2-4(a). 交流阻抗之實部與虛部,與頻率以三維方式作圖,其中A面即為奈奎斯特圖,B面及C面雖非波德圖,但為相似的表達方式,可以應分析需求使用;而|Z|和Ψ對頻率作圖則為波德圖(D與E).webp) 圖 2-2-4(b). 以電阻電容並聯電路之實際量測,示範在圖2-2-4(a)中,A~E各圖形
圖 2-2-4(b). 以電阻電容並聯電路之實際量測,示範在圖2-2-4(a)中,A~E各圖形.webp)

.webp)

.webp)

.webp)

.webp)

.webp) 圖 2-2-5 (b). Warburg impedance的等效電路
圖 2-2-5 (b). Warburg impedance的等效電路左圖.webp)
.webp)
左圖.webp)
右圖.webp)
右圖-11.webp)
右圖-11.webp)
右圖-11.webp)